Dec 14, 2019
Ask Ethan: Could Octonions Unlock How Reality Really Works?
Posted by Quinn Sena in categories: education, mathematics, physics
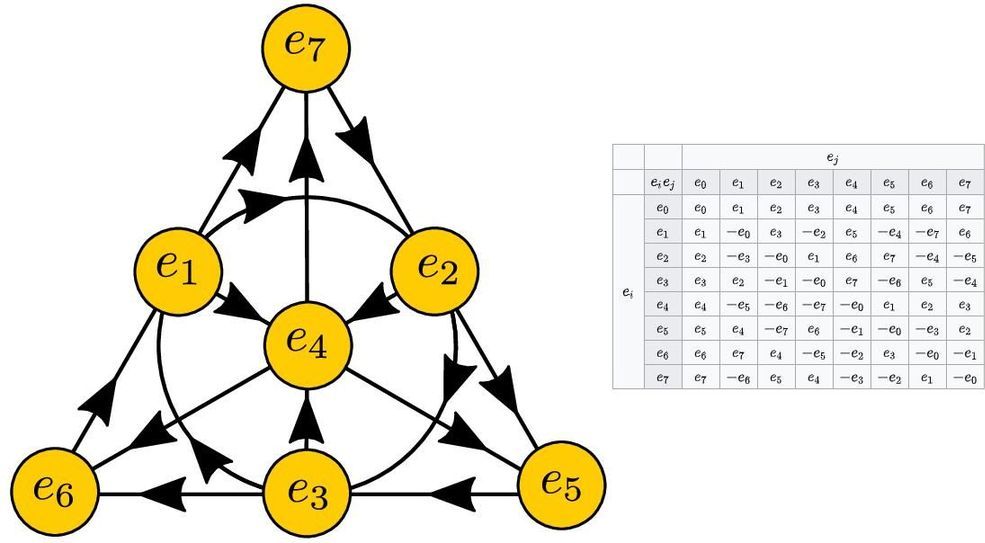
The octonions themselves will never be “the answer” to how reality works, but they do provide a powerful, generalized mathematical structure that has its own unique properties. It includes real, complex, and quaternion mathematics, but also introduces fundamentally unique mathematical properties that can be applied to physics to make novel — but speculative and hitherto unsupported — predictions.
Octonions can give us and idea of which possibilities might be compelling to look at in terms of extensions to known physics and which ones might be less interesting, but there are no concrete observables predicted by the octonions themselves. Pierre Ramond, my former professor who taught me about octonions and Lie groups in physics, was fond of saying, “octonions are to physics what the Sirens were to Ulysses.” They definitely have an allure, but if you dive in, they may drag you to a hypnotic, inescapable doom.
Their mathematical structure holds an incredible richness, but nobody knows whether that richness means anything for our Universe or not.