Lifeboat Foundation: Safeguarding Humanity
Toggle light / dark theme

Blog

Category: physics

Maxwell–Boltzmann distribution generalized to real gases

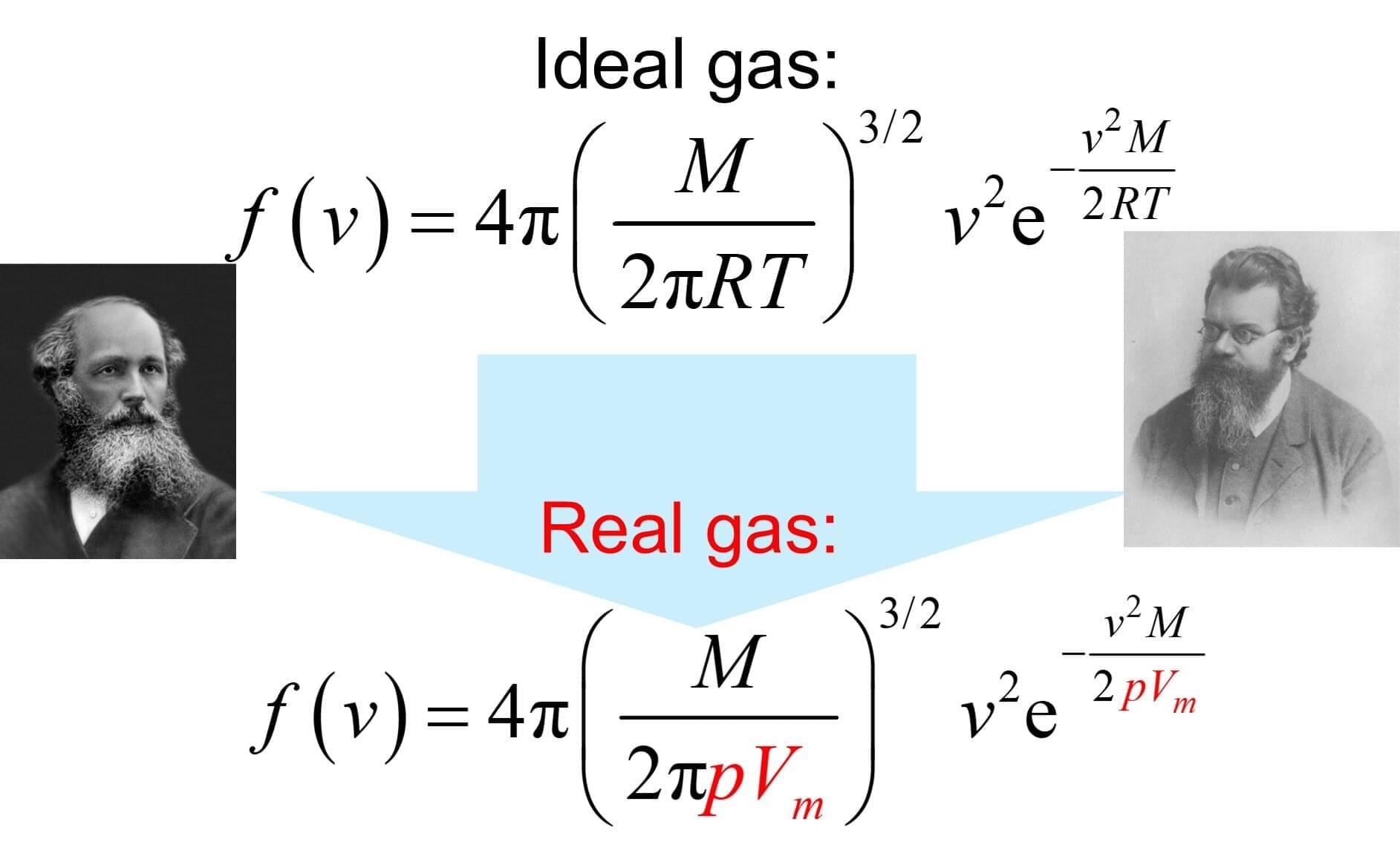
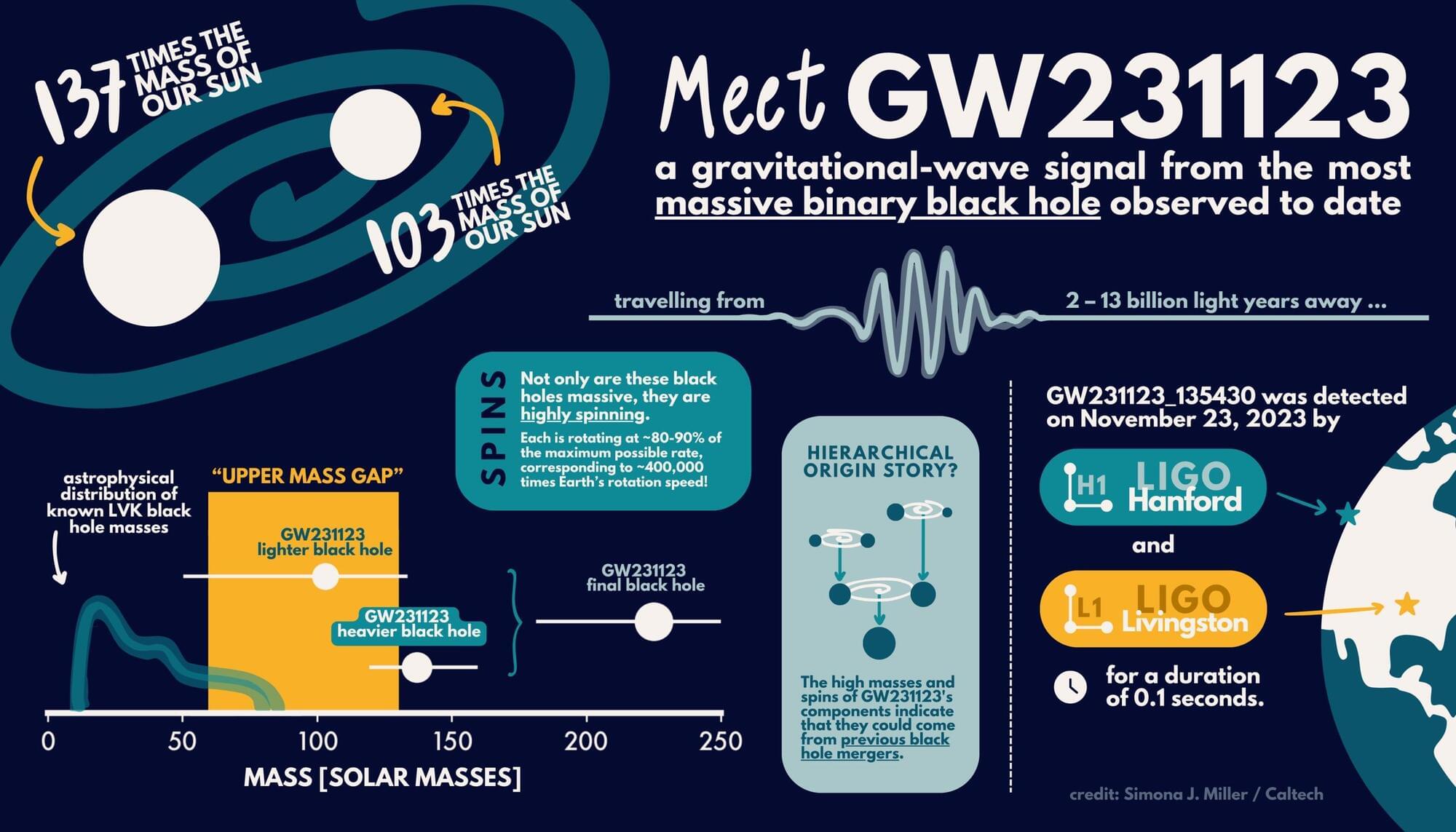
The Maxwell–Boltzmann distribution describes the probability distribution of molecular speeds in a sample of an ideal gas. Introduced over 150 years ago, it is based on the work of Scottish physicist and mathematician James Clerk Maxwell (1831–1879) and Austrian mathematician and theoretical physicist Ludwig Boltzmann (1844–1906).

Today, the distribution and its implications are commonly taught to undergraduate students in chemistry and physics, particularly in introductory courses on or statistical mechanics.

In a recent theoretical paper, I introduced a novel formula that extends this well-known distribution to real gases.

This aerospike rocket engine designed by generative AI just completed its first hot fire test

The reason these aerospike style engines haven’t been used more in the past is they’re difficult to design and make. While generally thought of as having the potential to be more efficient, they also require intricate cooling channels to help keep the spike cool. CEO and Co-Founder of LEAP 71, Josefine Lissner, credits the company’s computational AI, Noyron, with the ability to make these advancements.

“We were able to extend Noyron’s physics to deal with the unique complexity of this engine type. The spike is cooled by intricate cooling channels flooded by cryogenic oxygen, whereas the outside of the chamber is cooled by the kerosene fuel.” Said Lissner “I am very encouraged by the results of this test, as virtually everything on the engine was novel and untested. It’s a great validation of our physics-driven approach to computational AI.”

Lin Kayser, Co-Founder of LEAP 71, also believes the AI was paramount in achieving the complex design, explaining “Despite their clear advantages, Aerospikes are not used in space access today. We want to change that. Noyron allows us to radically cut the time we need to re-engineer and iterate after a test and enables us to converge rapidly on an optimal design.”

Blades of light: A tabletop method for generating megatesla magnetic fields

Researchers at The University of Osaka have developed a novel method for generating ultra-high magnetic fields via laser-driven implosions of blade-structured microtubes. This method achieves field strengths approaching one megatesla—a breakthrough in compact, high-field plasma science.

Ultrastrong magnetic fields approaching the megatesla regime—comparable to those found near strongly magnetized or —have now been demonstrated in theory using a compact, laser-driven setup.

A team led by Professor Masakatsu Murakami at The University of Osaka has proposed and simulated a unique scheme that uses micron-sized hollow cylinders with internal blades to achieve these field levels. The research is published in the journal Physics of Plasmas.

Patterns of patterns: Exploring supermoiré engineering

A few years ago, physicists were surprised to learn that stacking and subtly twisting two atomically thin layers of an electronic material like graphene creates a pattern that changes the material’s properties and can even turn it into a superconductor. This superimposed grid, like what would emerge if two window screens were laid slightly askew, is called a moiré pattern.

But why stop there? It turns out adding a third layer, with each layer twisted at slightly different angles, produces even more complex interferences known as supermoiré patterns (aka moiré of moiré). The supermoiré pattern induces profound changes in how electrons move through the material, but until recently, scientists had had trouble measuring exactly what changes occur and why.

Now, applied physicists in the Harvard John A. Paulson School of Engineering and Applied Sciences (SEAS) have used a specially designed microscope to probe the properties of supermoiré patterns in trilayer graphene to an extent that was never possible before. Using their microscope, they saw many new states of matter in which electrons would get stuck or form unusual groups, leading to changes in the entire system’s electronic behavior and opening doors to studying layered materials with precisely controllable properties.

LIGO-Virgo-KAGRA detect most massive black hole merger to date

The LIGO-Virgo-KAGRA (LVK) Collaboration has detected the merger of the most massive black holes ever observed with gravitational waves using the LIGO observatories. The powerful merger produced a final black hole approximately 225 times the mass of our sun. The signal, designated GW231123, was detected during the fourth observing run of the LVK network on November 23, 2023.

LIGO, the Laser Interferometer Gravitational-wave Observatory, made history in 2015 when it made the first-ever direct detection of , ripples in space-time. In that case, the waves emanated from a black hole merger that resulted in a final black hole 62 times the mass of our sun. The signal was detected jointly by the twin detectors of LIGO, one located in Livingston, Louisiana, and the other in Hanford, Washington.

Since then, the LIGO team has teamed up with partners at the Virgo detector in Italy and KAGRA (Kamioka Gravitational Wave Detector) in Japan to form the LVK Collaboration. These detectors have collectively observed more than 200 in their fourth run, and about 300 in total since the start of the first run in 2015.

“This AI Outperformed Human Scientists”: Tasked With Reinventing Gravitational Wave Detectors, It Designed 50 Revolutionary Models That Could Change Everything

IN A NUTSHELL 🚀 Researchers have developed an AI program named Urania that designs more effective gravitational wave detectors. 🌌 These new detectors could significantly enhance our ability to observe distant cosmic events, including black hole mergers and early universe phenomena. 🔍 The AI-designed detectors cover a wider frequency range, potentially increasing the universe’s observable

Record financing for Proxima Fusion

The Munich-based start-up Proxima Fusion, a spin-out from the Max Planck Institute for Plasma Physics, has raised €130 million in capital. The company plans to use the funds to finance the development of the world’s first stellarator-based fusion power plant, which is scheduled to be built in the 2030s. The investment represents the largest private financing round in the field of fusion energy in Europe to date. Proxima Fusion now has a total of more than €185 million in public and private funding at its disposal.

What Happens After Superintelligence? (with Anders Sandberg)

Anders Sandberg joins me to discuss superintelligence and its profound implications for human psychology, markets, and governance. We talk about physical bottlenecks, tensions between the technosphere and the biosphere, and the long-term cultural and physical forces shaping civilization. We conclude with Sandberg explaining the difficulties of designing reliable AI systems amidst rapid change and coordination risks.

Learn more about Anders’s work here: https://mimircenter.org/anders-sandberg.

Timestamps:
00:00:00 Preview and intro.
00:04:20 2030 superintelligence scenario.
00:11:55 Status, post-scarcity, and reshaping human psychology.
00:16:00 Physical limits: energy, datacenter, and waste-heat bottlenecks.
00:23:48 Technosphere vs biosphere.
00:28:42 Culture and physics as long-run drivers of civilization.
00:40:38 How superintelligence could upend markets and governments.
00:50:01 State inertia: why governments lag behind companies.
00:59:06 Value lock-in, censorship, and model alignment.
01:08:32 Emergent AI ecosystems and coordination-failure risks.
01:19:34 Predictability vs reliability: designing safe systems.
01:30:32 Crossing the reliability threshold.
01:38:25 Personal reflections on accelerating change.