Erbium and similar elements provide a wide range of electronic “handles” for manipulating atoms in many-body quantum experiments.
Scientists have a problem with cosmic rays—they produce too many muons at the Earth’s surface. Cascades of muons are byproducts of high-energy cosmic rays as they collide with nuclei in the upper atmosphere, and scientists see more muons at Earth’s surface than standard physics models predict.
Vorticity, a measure of the local rotation or swirling motion in a fluid, has long been studied by physicists and mathematicians. The dynamics of vorticity is governed by the famed Navier-Stokes equations, which tell us that vorticity is produced by the passage of fluid past walls. Moreover, due to their internal resistance to being sheared, viscous fluids will diffuse the vorticity within them and so any persistent swirling motions will require a constant resupply of vorticity.
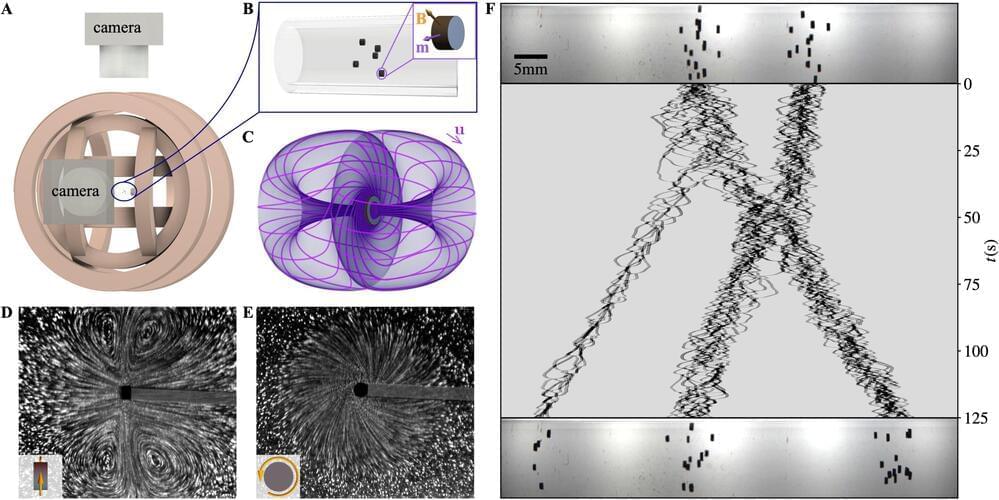
Physicists at the University of Chicago and applied mathematicians at the Flatiron Institute recently carried out a study exploring the behavior of viscous fluids in which tiny rotating particles were suspended, acting as local, mobile sources of vorticity. Their paper, published in Nature Physics, outlines fluid behaviors that were never observed before, characterized by self-propulsion, flocking and the emergence of chiral active phases.
“This experiment was a confluence of three curiosities,” William T.M. Irvine, a corresponding author of the paper, told Phys.org. “We had been studying and engineering parity-breaking meta-fluids with fundamentally new properties in 2D and were interested to see how a three-dimensional analog would behave.
There are over 30,000 weather stations in the world, measuring temperature, precipitation and other indicators often on a daily basis. That’s a massive amount of data for climate researchers to compile and analyze to produce the monthly and annual global and regional temperatures (especially) that make the news.
Now researchers have unleashed artificial intelligence (AI) on these datasets to analyze temperature extremes in Europe, finding excellent agreement compared to existing results that used traditional methods, and as well have uncovered climate extremes not previously known. Their work has been published in Nature Communications.
With the world’s climate changing rapidly, it is important to know how temperature and precipitation extremes are changing, so planners can adapt to the extremes here now and to what’s coming.
Oxford University researchers have made a significant step toward realizing a form of “biological electricity” that could be used in a variety of bioengineering and biomedical applications, including communication with living human cells. The work was published on 28 November in the journal Science.
Iontronic devices are one of the most rapidly-growing and exciting areas in biochemical engineering. Instead of using electricity, these mimic the human brain by transmitting information via ions (charged particles), including sodium, potassium, and calcium ions.
Ultimately, iontronic devices could enable biocompatible, energy-efficient, and highly precise signaling systems, including for drug-delivery.
Kuhn’s taxonomy of consciousness connects various theories to deep questions about human existence and AI, based on his extensive dialogue with over 200 experts.
“Out of meat, how do you get thought? That’s the grandest question,” said philosopher Patricia Churchland to Robert Lawrence Kuhn, the producer and host of the acclaimed PBS program Closer to Truth and member of FQxI’s scientific advisory council.
Kuhn has now published a comprehensive taxonomy of proposed solutions and theories regarding the hard problem of consciousness. His organizing framework aims to assess their impact on meaning, purpose, and value, as well as on AI consciousness, virtual immortality, survival beyond death, and free will. His work, titled ‘Landscape of Consciousness,’ appeared in the August 2024 issue of the journal Progress in Biophysics and Molecular Biology.
There’s a mineral so rare that only one specimen of it has ever been found in the entire world.
It’s called kyawthuite (cha-too-ite), a tiny, tawny-hued grain weighing just a third of a gram (1.61 carats). On first glance, you might mistaken it for amber or topaz; but the unassuming mineral speck has value beyond measure.
The stone itself was purchased in 2010 at a market in Chaung-gyi in Myanmar by gemologist Kyaw Thu, who thought the raw gem was a mineral called scheelite. After he faceted the stone, though, he realized that he was looking at something unusual.
In 2015, David Hole was prospecting in Maryborough Regional Park near Melbourne, Australia.
Armed with a metal detector, he discovered something out of the ordinary – a very heavy, reddish rock resting in some yellow clay.
It’s no secret: when we savour a delicious piece of fish or a platter of seafood, we’re not just consuming valuable omega-3s and vitamin D. Alongside these benefits come less appetising elements – countless micro– and nano-plastics.
These plastic particles, measuring less than 5 millimetres, enter our oceans through human waste and penetrate the food chain. According to an Ifremer study, around 24,400 billion microplastics are floating on the ocean’s surface.
These particles are found in all marine organisms – from microalgae to fish, which occupy higher levels of the food chain. This phenomenon not only threatens marine ecosystems but also raises concerns about potential risks to human health.
Can you pass me the whatchamacallit? It’s right over there next to the thingamajig.
Many of us will experience “lethologica”, or difficulty finding words, in everyday life. And it usually becomes more prominent with age.
Continue reading “Scientists Discover a Speech Trait That Foreshadows Cognitive Decline” »
