Information theory, the science of message communication44, has also served as a framework for model-free causality quantification. The success of information theory relies on the notion of information as a fundamental property of physical systems, closely tied to the restrictions and possibilities of the laws of physics45,46. The grounds for causality as information are rooted in the intimate connection between information and the arrow of time. Time-asymmetries present in the system at a macroscopic level can be leveraged to measure the causality of events using information-theoretic metrics based on the Shannon entropy44. The initial applications of information theory for causality were formally established through the use of conditional entropies, employing what is known as directed information47,48. Among the most recognized contributions is transfer entropy (TE)49, which measures the reduction in entropy about the future state of a variable by knowing the past states of another. Various improvements have been proposed to address the inherent limitations of TE. Among them, we can cite conditional transfer entropy (CTE)50,51,52,53, which stands as the nonlinear, nonparametric extension of conditional GC27. Subsequent advancements of the method include multivariate formulations of CTE45 and momentary information transfer54, which extends TE by examining the transfer of information at each time step. Other information-theoretic methods, derived from dynamical system theory55,56,57,58, quantify causality as the amount of information that flows from one process to another as dictated by the governing equations.
Another family of methods for causal inference relies on conducting conditional independence tests. This approach was popularized by the Peter-Clark algorithm (PC)59, with subsequent extensions incorporating tests for momentary conditional independence (PCMCI)23,60. PCMCI aims to optimally identify a reduced conditioning set that includes the parents of the target variable61. This method has been shown to be effective in accurately detecting causal relationships while controlling for false positives23. Recently, new PCMCI variants have been developed for identifying contemporaneous links62, latent confounders63, and regime-dependent relationships64.
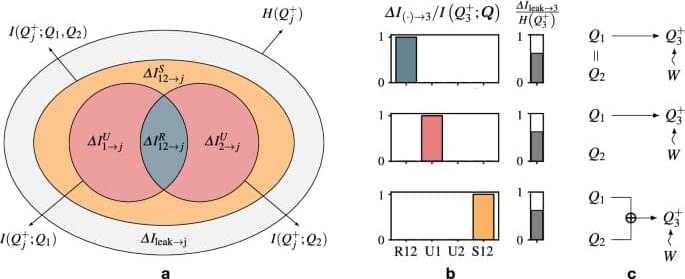
The methods for causal inference discussed above have significantly advanced our understanding of cause-effect interactions in complex systems. Despite the progress, current approaches face limitations in the presence of nonlinear dependencies, stochastic interactions (i.e., noise), self-causation, mediator, confounder, and collider effects, to name a few. Moreover, they are not capable of classifying causal interactions as redundant, unique, and synergistic, which is crucial to identify the fundamental relationships within the system. Another gap in existing methodologies is their inability to quantify causality that remains unaccounted for due to unobserved variables. To address these shortcomings, we propose SURD: Synergistic-Unique-Redundant Decomposition of causality. SURD offers causal quantification in terms of redundant, unique, and synergistic contributions and provides a measure of the causality from hidden variables. The approach can be used to detect causal relationships in systems with multiple variables, dependencies at different time lags, and instantaneous links. We demonstrate the performance of SURD across a large collection of scenarios that have proven challenging for causal inference and compare the results to previous approaches.