Lifeboat Foundation

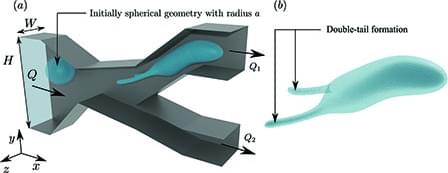
The physics of drop motion in microchannels is fundamental to provide insights when designing applications of drop-based microfluidics. In this paper, we develop a boundary-integral method to simulate the motion of drops in microchannels of finite depth with flat walls and fixed depth but otherwise arbitrary geometries. To reduce computational time, we use a moving frame that follows the droplet throughout its motion. We provide a full description of the method, including our channel-meshing algorithm, which is a combination of Monte Carlo techniques and Delaunay triangulation, and compare our results to infinite-depth simulations. For regular geometries of uniform cross section, the infinite-depth limit is approached slowly with increasing depth, though we show much faster convergence by scaling with maximum vs average velocities. For non-regular channel geometries, features such as different branch heights can affect drop partitioning, breaking the symmetric behavior usually observed in regular geometries. Moreover, non-regular geometries also present challenges when comparing the results for deep and infinite-depth channels. To probe inertial effects on drop motion, the full Navier–Stokes equations are first solved for the entire channel, and the tabulated solution is then used as a boundary condition at the moving-frame surface for the Stokes flow inside the moving frame. For moderate Reynolds numbers up to Re = 5, inertial effects on the undisturbed flow are small even for more complex geometries, suggesting that inertial contributions in this range are likely small. This work provides an important tool for the design and analysis of three-dimensional droplet-based microfluidic devices.